Qubits and gates
How do quantum gates actually work? Visualizations can help us to understand what’s going on inside the box.
A single-qubit gate
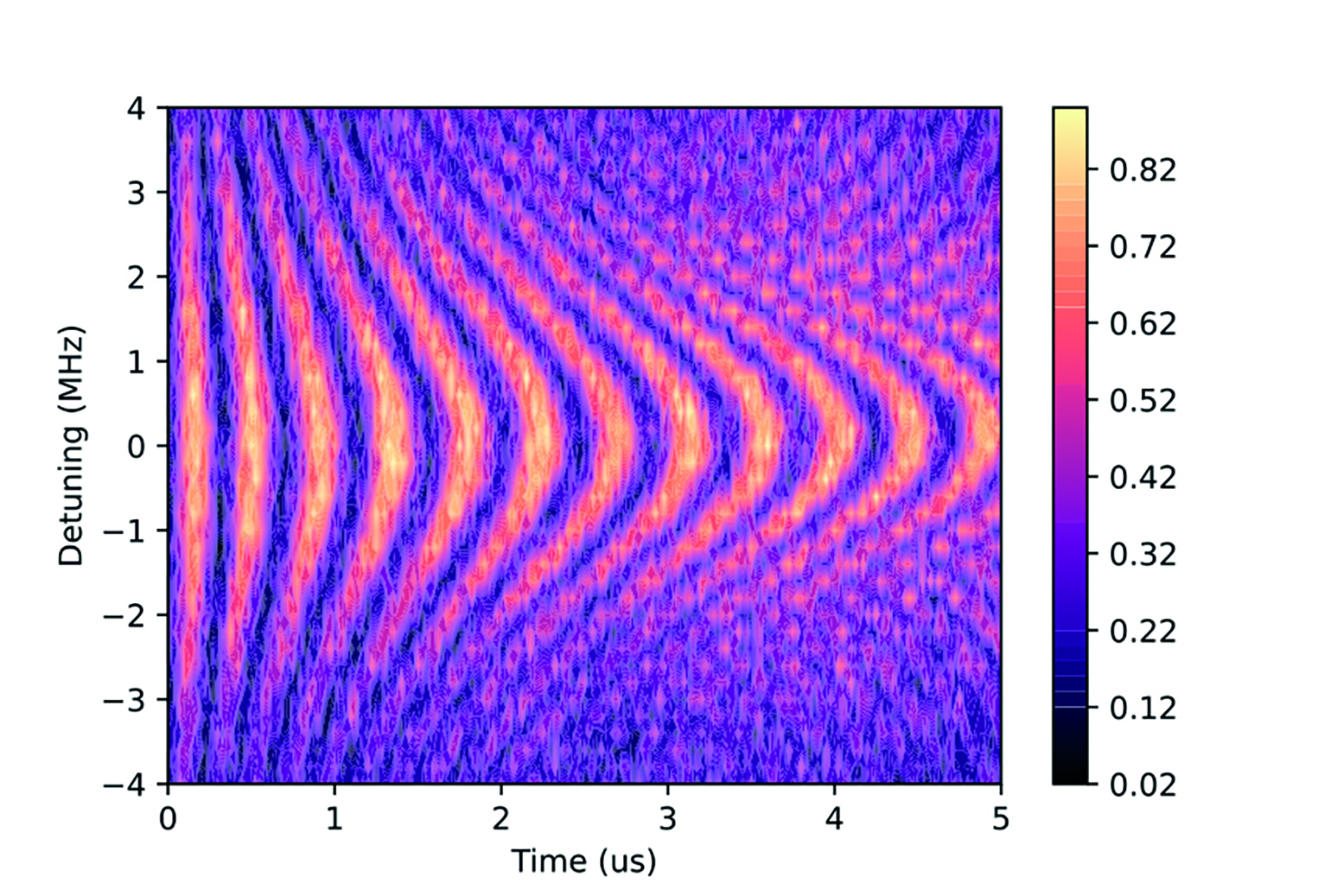
How do scientists and engineers actually perform a quantum operation, such as an X-gate? Let’s consider a spin qubit. A spin behaves a bit like a top spinning around its axis. When a top is spinning on a table, it’s quite robust against small pokes and prods. Similarly, a spin qubit won’t easily flip over. However, if we apply a signal that has the same frequency as the spin qubit, the spin will begin to rotate from its “up” (or “0”) state to its “down” (or “1”) state. The longer the pulse is applied, the more the spin will rotate. The larger the pulse, the faster the spin will rotate. This spin-flipping phenomenon is known as Rabi oscillation.
The plot shows the state of the spin for various pulse durations and frequencies. We can see that only pulses with exactly the same frequency as the qubit – known as its resonant frequency – will cause perfect flips. To perform an X-gate, for example, this frequency must be tuned for each qubit. Then, the correct pulse duration can be selected such that the spin flips exactly halfway. In this plot, we refer to the difference between the frequency we apply and the qubit’s resonant frequency as detuning, shown in the plot on the Y axis.
The colors in the plot represent the probability of the qubit’s state being “up” (0), as shown by the legend on the right of the graph. When a point on the plot is dark purple, the qubit’s state is most likely to be “up”; likewise, the light yellow points mean the qubit’s state is most likely to be “down” (1). The contrast between light and dark is clearest around the center of the Y-axis – so where detuning is zero, and we are applying the qubit’s resonant frequency. This shows us how making a qubit resonate results in clear, consistent “flips” between up (light) and down (dark).
Bloch Spheres
A Bloch sphere (shown above) is a common way of visualizing a single qubit’s current state. We do this by showing the state as a vector, starting from the center of the sphere, and pointing to somewhere on its surface. The top and bottom “poles” of the sphere are called basis states – usually “0” and “1”, or positive and negative. When we measure a qubit, we find out which of these two states the qubit is in.
A two-qubit gate
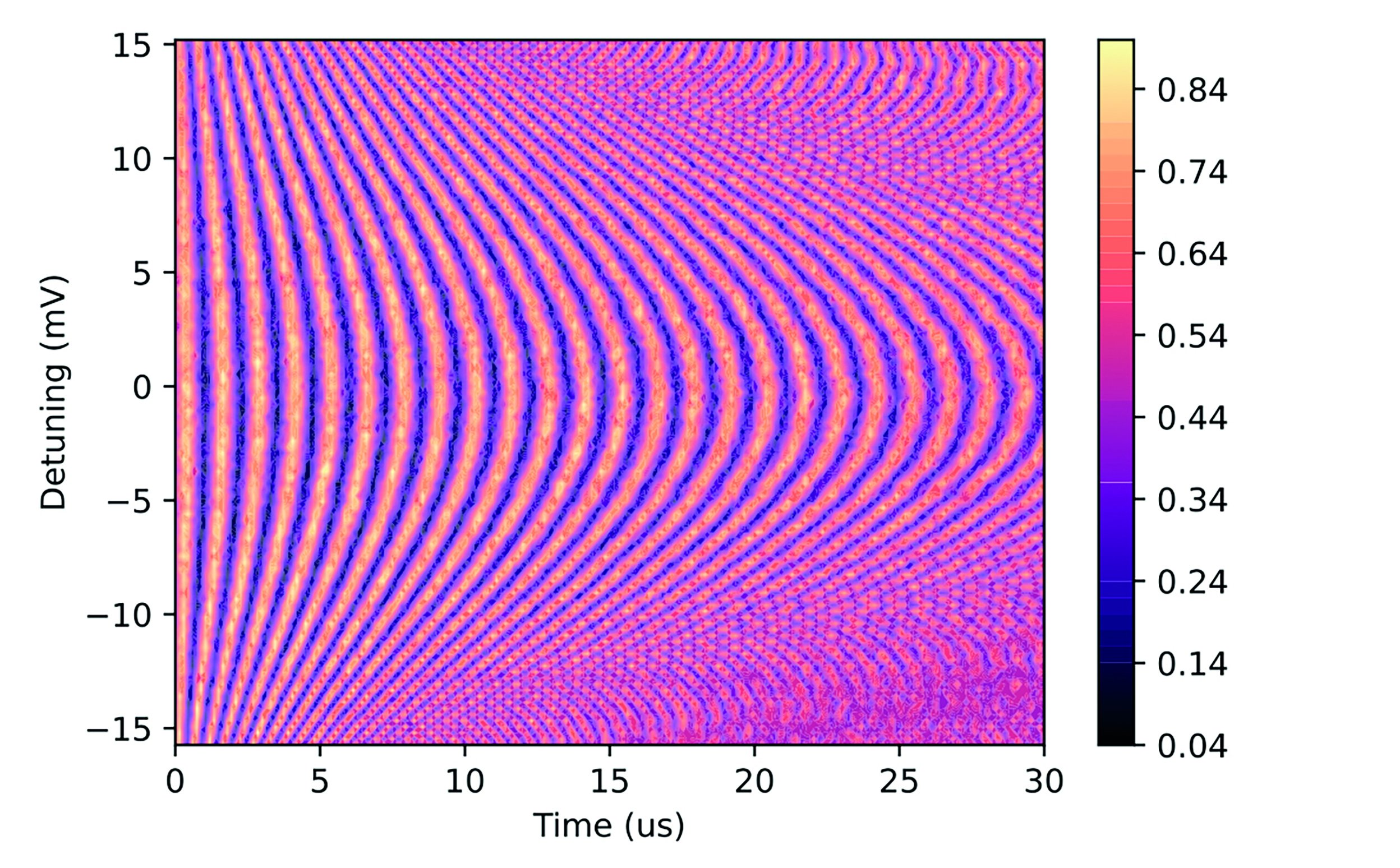
Quantum algorithms are built not only with single-qubit operations, but by using the interactions between multiple qubits as well.
Below is a plot of a two-qubit gate called a CPhase (controlled phase) gate. When two spins are captured in two adjacent wells, or quantum dots, they will exchange information about their state with one another. Unlike in the case of single qubit gates, no high-frequency pulses are needed here. The interaction is “turned on” when the barrier between the two electron spins is decreased such that the electrons move close to one another. Here, the amount of time that the barrier is moved down determines the duration of the two-qubit interaction.
Pulses with the exact same frequency as a qubit—known as its resonant frequency—will cause perfect flips.