Fault-tolerant computing

It takes more than just qubits to build a powerful, universal quantum computer.

Decoherence

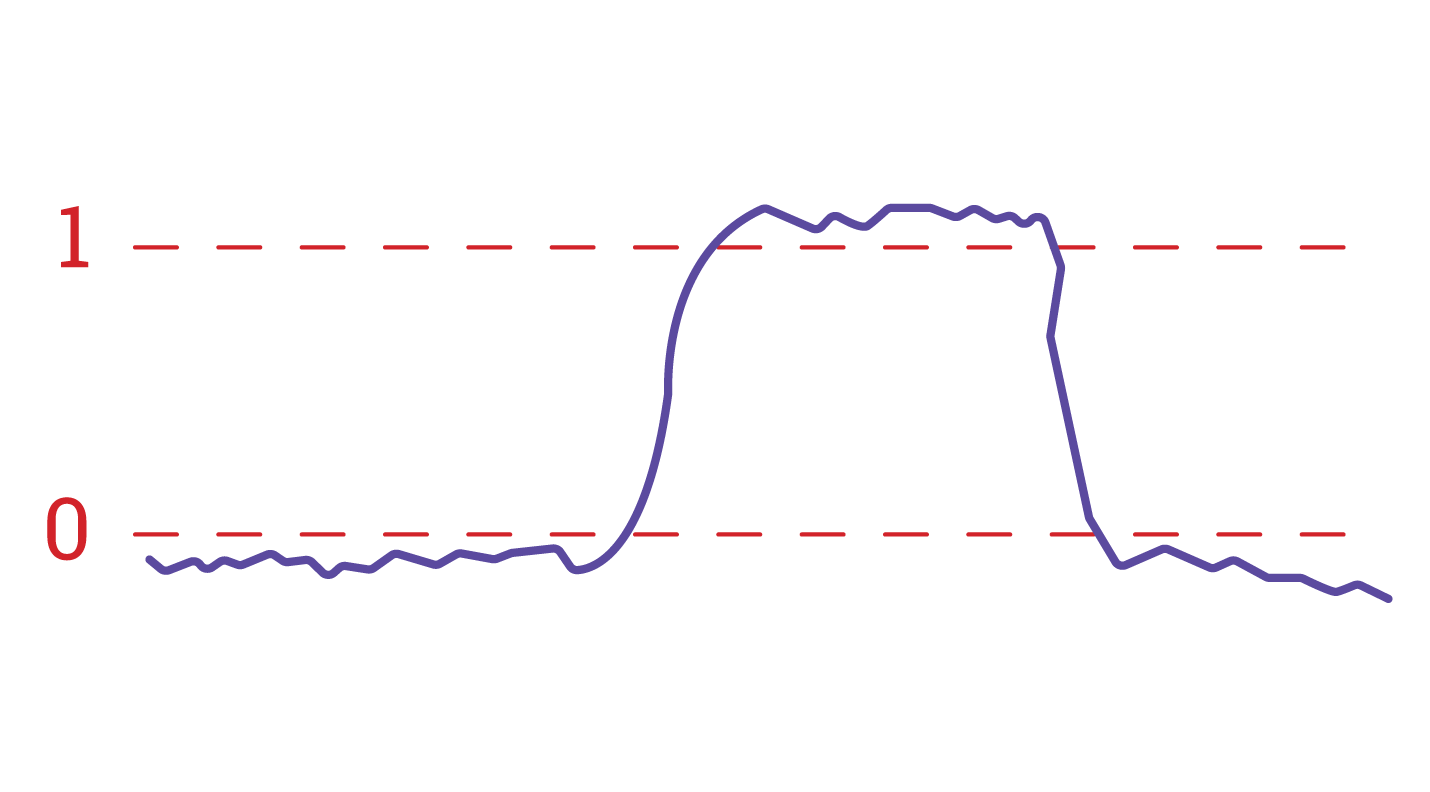
Qubits are extremely fragile, and this limits how long they are useful for quantum computing. For example, if a quantum calculation is expected to take 5 seconds, but the quantum computer has qubits with a coherence time – the time a qubit can hold its information – of 1 second, the result of the programme will be nonsense. Scientists and engineers call this decay in quality decoherence, and understanding it is essential to evaluate the power of quantum hardware.

Decoherence can be classified into two categories: relaxation and dephasing. Imagine a qubit as a coin spinning on a table. The relaxation time is how long it takes the spinning coin to fall down. The dephasing time is how long it takes us to lose track of how fast the coin is spinning. For real coins, these effects happen because the surface of the table is rough, and air resistance causes the coin to gradually slow down.

Qubits are sensitive to any disturbance, even as small as microscopic vibrations or cosmic rays from outer space. It is for this reason that qubits typically require extremely cold temperatures, which reduce the vibrations of atoms in materials, or high vacuum, which lowers the risk of unwanted particles bumping into the qubits.

Qubit Quality and Quantum Volume

It is tempting to conclude that qubits with a longer coherence time are better than those which decohere faster, but the reality is more nuanced. Qubits may last a long time if they’re very well isolated, but they must also be readily initialized, manipulated, and measured in order to build useful quantum computers. Accessibility and isolation are often at odds. Commonly, qubits with long lifetimes are also slow to operate. For this reason, a more meaningful measure of the power of a qubit is its quality factor, the ratio of how long a qubit lasts and how many operations can be performed with it during this time. IBM has encapsulated this idea with their coined term “Quantum Volume”, which measures the power of a quantum computer both by how many qubits it has and how many operations can be performed within the coherence time.

Error Correction

Classical computers, the ones we use in our day-to-day lives, rarely make mistakes. Sometimes it feels like they do, when your desktop freezes or a sent email vanishes in the ether. Practically speaking, however, this is because of a mistake in the instructions given to the computer, not because of an error in the semiconductor chips. The bits in a computer, the “0”s and “1”s representing classical information, are digital, and therefore rather insensitive to errors. If a “0” has to change into a “1” in a classical computer, and this is done with a slight mistake, the result still looks mostly like a “1” and is then treated as such.

Let’s imagine a computer that is really bad at flipping “0” to “1”. How can we prevent errors in our understanding of what this computer is supposed to do? The simplest answer is to let this computer not work on single bits “0” or “1” but on three bits “000” or “111” simultaneously. We can then assume that the computer wants to “0” to a “1” if it does so for at least two “0”s:

Now, even though there are plenty of mistakes, the error could be tolerated because the computer could get it right most of the time. Things aren’t so simple in the case of quantum computers for three reasons. First, the possible errors are continuous. For quantum computing, we don’t just care about flipping between “0” and “1”, we also care about the states in-between. Flipping too much or too little matters a lot.

Second, there is a fundamental law in quantum computing that implies that we can’t duplicate qubits (this law is known as the No-Cloning Theorem). This takes away the possibility of copying a qubit multiple times, then trying the operation on each copy, as we showed above.

Last, there is the difficulty that measuring a qubit destroys superposition. As soon as we look at a qubit, we see exactly “0” or exactly “1”. If we suspect an error may have taken place, we can’t simply look at the qubit to check without ruining the computation.

These sound like insurmountable obstacles, but by using the powerful techniques of quantum error correction, inevitable errors can be detected and corrected without running into any of these three roadblocks.