Quantum circuits
What does quantum computing look like? Exploring the basic units of quantum algorithms is a good place to start.
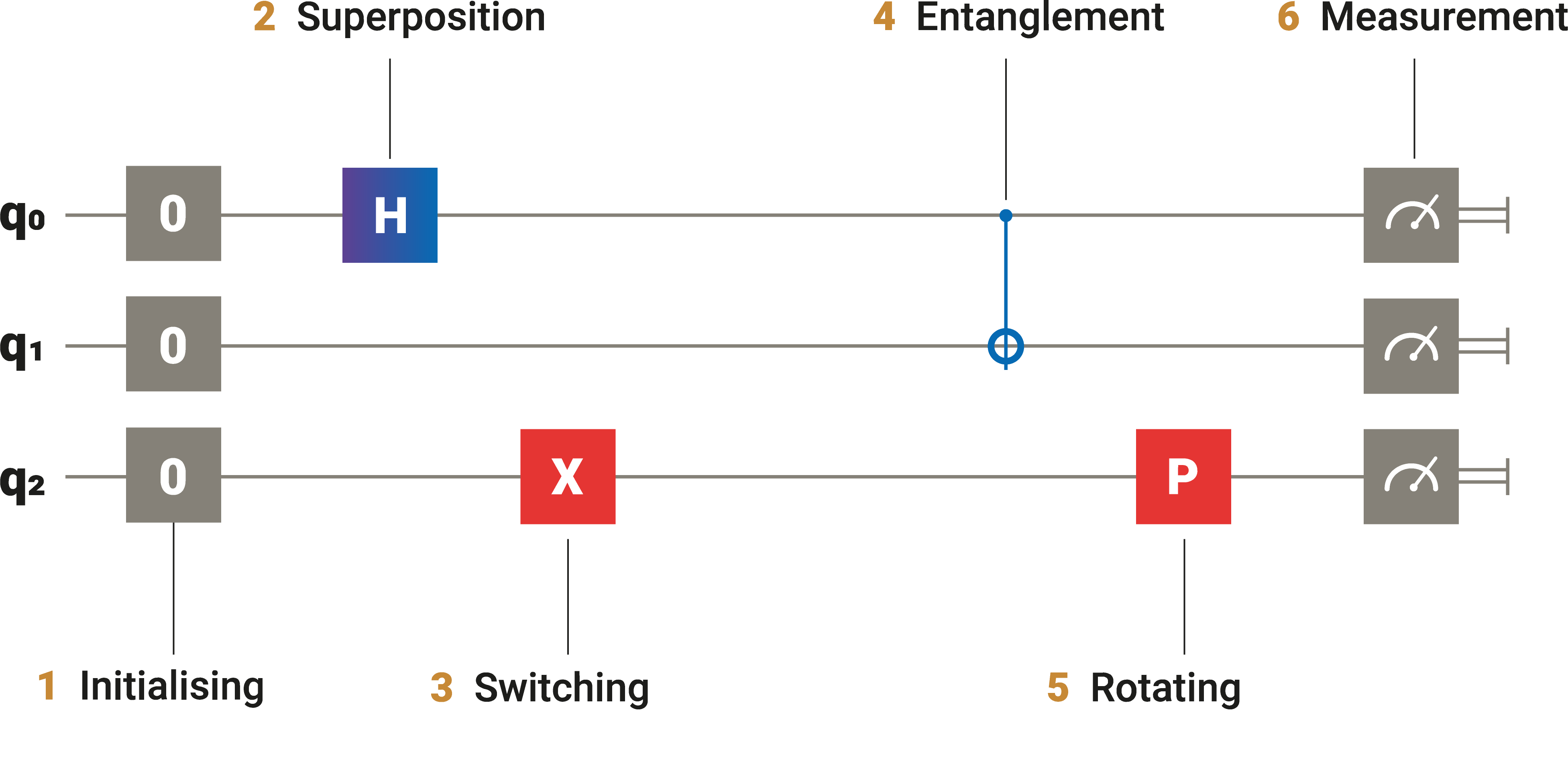
-
Each qubit in a circuit is denoted by a vector, representing its state. Here, all three qubits' initial states are set to "0".
-
The squares on each line represent gates. A gate is a transformation applied to a qubit. This one - the Hadamard gate - puts a qubit in superposition.
-
This gate, known as the Pauli-X gate (or simply X-gate), 'flips' the state of a qubit from "0" to "1" or "1" to "0". More specifically, it switches the amplitudes of the states "0" and "1".
-
This line represents a CNOT-gate, which is conditional. If qubit 0's state equals "1", it applies the same transformation as the X-gate to qubit "1". Because qubit "0" is in superposition, this causes qubits "0" and "1" to be entangled.
-
This gate, known as the phase gate (or simply P-gate), rotates the vector representing a qubit's state around the z-axis by a specified amount.
-
Measuring a qubit makes it collapse into one defined state (known as an eigenstate). The measured value we get reflects this state.
Building Quantum Circuits
Quantum circuits are made by combining multiple successive gates. Cumulatively, they manipulate qubits – both individually and in multiples – to perform complex calculations known as algorithms. Shor’s algorithm, shown below, is used to factorize integers.
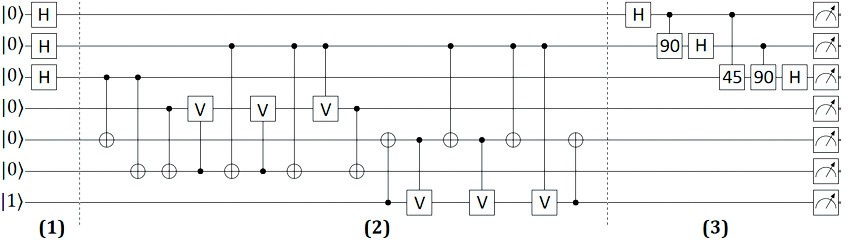
A quantum computing interface
Most quantum programming frame-works offer interfaces which represent the qubit operations as shown in the image on this and the previous page”. In such a diagram, each line represents one qubit, which in this case all start in “0”. The different squares indicate manipulation of a qubit via a gate. The H gate, for example, creates a superposition from the “0” state, whereas the X gate flips a qubit from “0” to “1” and vice versa.
Lastly, we see connections between different qubits. These indicate a conditional gate, in which depending on the state of a neighbor we do or do not manipulate the qubit itself.