Factorization and encryption
Quantum computing could revolutionise the way we approach calculations—but can it really break modern encryption?
What is factorization?
Factorization is the process where a number is written as a product of smaller numbers. For instance, consider the number 24. 24 can be represented by 1x24, 2x12, 3x8, or 4x6. 24 is rather a small number, so writing down all possible factorizations is straightforward. But for larger numbers, how can we know that we have found all of the possibilities? One option is to continue factoring until all of the factors are prime. That is, each number has no factors other than 1 and itself. In our case, 24=2x2x2x3. All possible factorizations can be constructed from this list of prime numbers. For example, 24 = (2x2)x(2x3) = 4x6. The prime factorization of a number is like its fingerprint – it is unique to each one.
A difficult problem
What if we wanted to factor 49,189,447? This might take some time, because it can only be written as a product of two prime numbers: 6221x7907. Surely, a classical computer would be able to tackle this problem by trying a list of possibilities: 2, 3, 5, 7, and so on, until it found the correct numbers. But there are infinite prime numbers! The largest found to date (in 2018) has 24,862,048 digits when written down. If someone were to multiply this prime number with another massive one, even modern supercomputers wouldn’t be able to find the 2 factors.
There’s something peculiar about the asymmetry of this problem. Multiplying the numbers is easy, even for very large numbers, but factorization seems to be incredibly difficult. This is an instance of a one-way function, a mathematical problem that’s easy to proceed in one direction but hard to reverse. One-way functions are incredibly useful for keeping digital secrets. If you’ve ever made an online payment or sent a WhatsApp message, a one-way function has been used to secure your data. The most common example, RSA encryption, directly relies on the idea that factorization is computationally inefficient.
Shor’s Algorithm
This is where quantum computing comes in: a quantum computer can efficiently factor large numbers. For example, factoring a 600 digit number with the state-of-the-art classical techniques would require about a billion years. A large quantum computer may take a few hours. Why is this so? The answer, in a nutshell, is that the mathematics that describes how quantum computers work is also very good at describing the periodicity of complicated functions. This fortunate coincidence means that quantum computers can tackle certain mathematical problems that contemporary classical computers aren’t able to grapple with. Factorization is the most famous of these mathematical problems, and the quantum program which solves the problem is called Shor’s algorithm, named after its inventor in 1994.
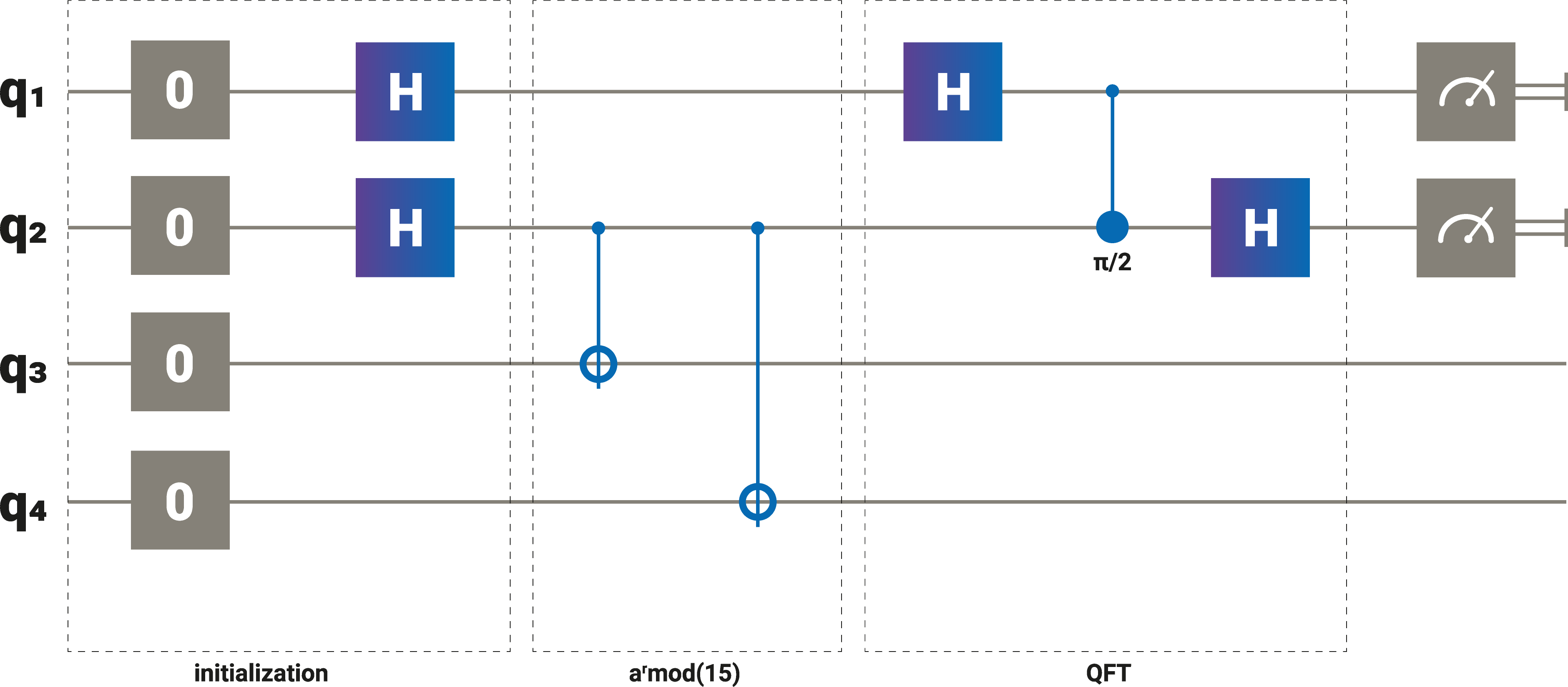
Perspective
Shor’s algorithm has become the crown jewel of quantum computing for two reasons. First, factorization is notoriously difficult, and the ability of quantum computers to excel at this problem over their classical counterparts has become symbolic of the supposed power of quantum information. Second, the existence of a quantum computer large enough to break RSA encryption would have profound implications for modern technology. This latter point raises an important ethical issue: why should society desire to build a device that would threaten to hack valuable personal, financial, and military data? For one thing, as with all powerful technologies, it’s not something that you want to let your adversary have exclusive access to. More importantly, there is a lot more societal good that quantum technology could do – as described in this magazine – including enabling a generation of even more informationally-secure devices and communication strategies.
The threat of quantum computers with respect to modern encryption is often overstated in popular science. In order to factor meaningfully large numbers, a very large number of physical qubits is required – present estimates place this in the range of several million. This is still far ahead of present quantum processors which operate with fewer than 100 qubits. This gives plenty of time for cryptographers to devise new post-quantum encryption schemes which are secure against large-scale quantum computers.
Shor’s algorithm serves as the most striking example of the potential for quantum technology when complemented with human ingenuity. It is one of the few problems where we know with certainty that a quantum computer can outperform the best classical algorithm at present. However, it will take a large, error-corrected quantum computer to be able to execute Shor’s algorithm in the long term.
The Fine Print
Shor’s algorithm requires a quantum computer with a large number of qubits. The main reason is the need for error correction. It has been estimated that to break typical RSA encryption a quantum computer with 20 million qubits would be needed. This greatly exceeds today’s quantum machines.


