Gravity
We aim to develop new methodologies and algorithms for modelling the static and time-variable gravity field for applications in environmental science and engineering.
Gravity is a fundamental force, which mirrors mass distribution and mass redistribution in the Earth system, and, as such, is an important source of information used in various Earth and Engineering sciences. In geophysics it is used to recover rock densities, to build accurate geological models for mineral and hydrocarbon exploration, and to improve our knowledge of the Earth’s behaviour and evolution at the global scale. In oceanography, glaciology, and hydrology, gravity is used to observe variations in ocean currents, the melting of ice sheets, and variations of continental water storage. In geodesy, surfaces of constant gravity potential serve as reference surfaces for national height systems.
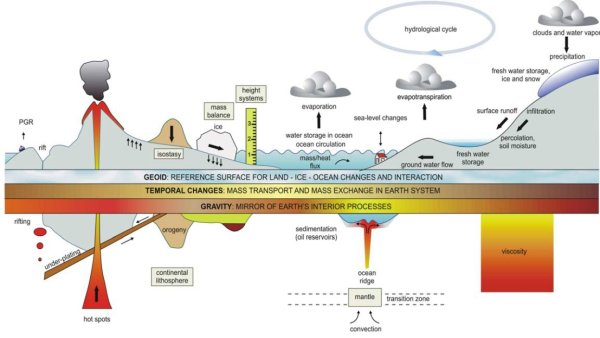
The interrelation between gravity/temporal gravity variations and mass distribution/transport (from Ilk et al. 2005).
When modelling the Earth’s gravity field on global to local scales, we follow an operational approach in which observations are coupled to a set of model parameter that are estimated using weighted least-squares techniques. Weighted least-squares techniques have many advantages; they allow the inclusion of noise covariance matrices, improve them using variance component estimation techniques, provide variance-covariance information about gravity field functionals and allow the use of statistical hypothesis testing to test the validity of the mathematical model. The development of efficient algorithms is a prerequisite not only for least-squares parameter estimation, but also for outlier detection algorithms, noise modelling, error propagation, and validation. Over the last 20 years, we have developed methodologies and algorithms for optimal data weighting of observation groups and outlier detection, frequency-dependent data weighting, and numerically efficient error propagation. We applied these using satellite, airborne, and/or terrestrial data as input and developed novel applications of static and time-varying gravity in continental hydrology, glaciology, hydrography, hydrocarbon reservoir modelling, solid Earth geophysics, and geodesy.
In the coming years, we will continue our efforts on time-varying gravity field modelling on the basis of satellite gravity data from GRACE, GRACE Follow-On, and other suitable satellites. One of our main goals is to produce tailored, optimally-filtered products tailored for specific applications in terms of spatial parameterisation, temporal parameterisation, and expected stochastic properties of the signal, which facilitates the accurate modelling of mass redistribution in the Earth’s system. We will continue our research on the estimation of low-degree spherical harmonic coefficients describing global gravity field features and geocentre motion by exploiting appropriate combinations of various satellite data and geophysical models. We will continue studying the optimal set-up of future satellite gravity missions to be launched in 10 to 20 years from now, keeping in mind a variety of different applications of those missions. Finally, we will continue the investigation of the noise budgets of satellite gravity data which may facilitate both an improvement in processing of available data and a better design of future satellite gravity missions.
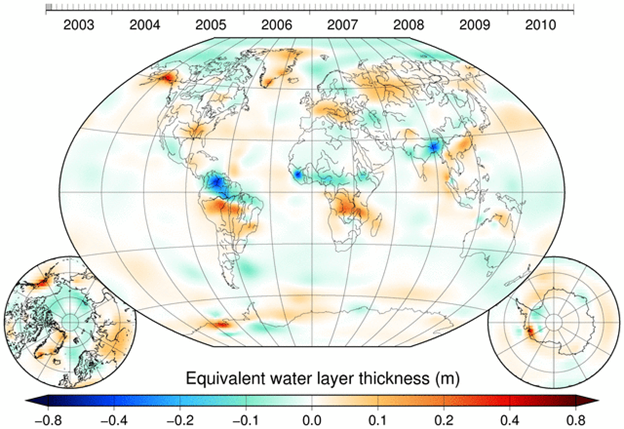
The Delft Mass Transport model comprises monthly time series of the global time-varying gravity field of the Earth.
Another research topic is regional gravity field modelling, which refers to the combination of satellite data with terrestrial, shipboard, and/or airborne data to achieve an improved spatial resolution for limited areas. The main application of regional gravity field modelling is the computation of quasi-geoid models that serve as reference surfaces for national height systems. Over the last ten years, we did pioneer work on the use of spherical radial base functions. We improved the processing of satellite radar altimeter data by the usage of dedicated and high-resolution hydrodynamic models in the computation of the dynamic topography corrections and the incorporation of the coloured noise when estimating the unknown parameters. We developed a new methodology to combine a gravimetric quasi-geoid with geometric height anomalies from GNSS, terrestrial gravity, and spirit levelling data. Based on these developments, we recently computed new quasi-geoid models for the Netherlands and Belgium with significant improvements upon the state-of-the-art models. Finally, recently we also developed a methodology that allows to combine a global gravity field model with local, high-resolution data sets in a statistically optimal way. Our main challenge for the next years is the computation of a regional quasi-geoid model at the 5 millimetre accuracy level.
Our research on gravimetry (the scientific discipline, which deals with instruments ('gravimeters') and procedures to measure the strength of the gravity field) focuses on i) the study of environmental processes such as atmospheric mass variations, tides, ocean loading, groundwater level variations, and soil moisture variations on gravity, and ii) the use of absolute gravity observations to control the absolute vertical motion of Normaal Amsterdams Peil (NAP), the reference of the Netherlands height system.