2. Grading
The grades you assign to your students can have far-reaching consequences for the continuation of their studies, scholarships and perhaps even on their careers. For that reason, it is important to know what to do when students obtained low grades because of an issue in the learning activities, assessment or grading process. This section will discuss grade calculation, and alterations that could be made after a test result analysis.
2.1. What is a grade?
The meaning of a grade is described in the Rules and Guidelines of the Board of Examiners of your programme. In general, it looks like this (R&G BoE master’s programmes MSc AP/CE/ LST/NB/SEC):
| 1.0-3.0 | 3.5-4.0 | 4.5-5.5 | 6.0 | 6.5-7.0 | 7.5-8.0 | 8.5-9.0 | 9.5-10.0 |
| Very poor | Poor | Unsatisfactory | Satisfactory | More than satisfactory | Good | Very good | Excellent |
In the Assessment Framework, this will be changed as follows:
| 1.0-1.5 | 2.0-2.5 | 3.0-3.5 | 4.0-4.5 | 5.0-5.5 | 6.0 | 6.5-7.0 | 7.5-8.0 | 8.5-9.0 | 9.5-10.0 |
| Very poor | Poor | Very unsatisfactory | unsatisfactory | Almost satisfactory | Satisfactory | Very satisfactory | Good | Very good | Excellent |
| Zeer slecht | Slecht | Ruim onvoldoende | Onvoldoende | Bijna voldoende | Voldoende | Ruim voldoende | Goed | Zeer goed | Uitmuntend |
In addition, course results can have the following values:
| NV | No show | Niet verschenen |
| if a student registered for an assessment but did not show up / did not hand in their work. | ||
| NVD | Did not pass | Niet voldaan |
| if a student e.g. did not receive sufficiently high assessment results, or did not participate in some parts. Consequently, a final grade cannot be calculated. | ||
| VR | Exemption | Vrijstelling |
| if the Board of Examiners granted an exemption. |
More importantly, the grade should relate to how well a student masters the learning objectives. If students demonstrate in a test that they master all learning objectives, they should be awarded a 10. Grade 1 is by Dutch convention the lowest grade that a student can obtain.
-
Grade 6.0 (or 5.75 before rounding) is the minimum pass grade. It implies that a student (on average) masters the learning objective at the minimum level to a) pass this course, and b) either start a course that builds upon this one, or in case there are none, c) master the related final attainments of the bachelor or master programme at the minimum required level and start their professional lives.
The course examiner should determine what the minimum level is at which the students will get this minimum pass grade (6.0). If a course is assessed with an exam with open questions, students often get a 6.0 if they receive 60% of the maximum score. Higher or lower percentages are also possible. Depending on the level of the questions, this may imply that a score of 6.0 implies that a student on average masters 60% of the learning objectives. They may not master some LOs at all, and may fully master other LOs. The exam averages this out.
For a master thesis that is assessed using an assessment sheet with scores on different criteria, it may imply that a student at least masters each individual criterion up to 50% (otherwise they would not have gotten their green light meeting), and that on average they master the criteria (that should be aligned with the learning objectives) at the minimum levels that are described in the assessment sheet. As
-
What about having one exam per learning objective, and requiring a 6.0 for each and every one of them? Or adding minimum levels for each criterion in assessment sheets of assignments and projects? Increasing the number of assessments?
There is a large objection against increasing the number of assessments. Nobody is able to create perfect assessments that perfectly measures the ‘true’ extend to which a student masters the learning objectives. The resulting ‘measurement error’ can be as high as two points on a grade from 1-10. If the number of tests and their accompanying minimum grades are increased, this increases the number of students who will fail the course incorrectly. Keep in mind that in the Rules & Guidelines of Examiners, in article 14, partial grades often require a minimum grade of 5.0.
Furthermore, students need to have resits for all these extra assessments, which would mean a lot of work for you. Furthermore, studying for resits or working on additions will steal away time from the other courses in the next period and therefore deteriorate student performance in the next period. Therefore, prevent creating unnecessary assessment hurdles.
On the other hand, it is important to gain insight on which learning objectives are accomplished by the students, and which not. Your course is, after all, part of a larger programme and qualification. Once a student graduates, it is assumed that the students have met the outcomes.
To conclude, be aware that introducing extra assessments will come with extra resits and additions, and therefore extra work for both students and teachers. Carefully balance the need to ascertain a minimum level for important learning objectives in the light of being able to successfully take follow-up courses and reaching the final attainments, with practicality for teachers (extra reviewing) and students (studyability of the next period in which they have to repair deficiencies).
-
Another question that is important to consider is the following: What guarantee does a pass give to the student about success in the rest of his study, and what guarantee does a pass give to your colleague that the student is able to successfully follow his or her course? This is called criterion validity.
Let us take a course on Electricity as an example. The course coordinator (also called the responsible lecturer) assumes the students have acquired the necessary mathematical skills to solve the equations, since it was a learning objective of the previous course. What can the course coordinator expect of her students on this ‘achieved’ mathematical learning objective? What if the students learnt this learning objective at the level of a 6? And what if the students skipped this learning objective in the last course and still managed to pass the exam?
It might be a good idea to talk to course coordinators of preceding and succeeding courses to discuss and (re)define the desirable level of a 6, so that they know what level they may expect from the students. It is unrealistic to assume that students master a learning objective of a previous course at the level of the learning objectives (a 10). Talking to colleagues will also enable you to give students advice on where to find information and (extra) exercises without you having to design the exercises and other material yourself.
2.2. Grade calculation
Now that we are clear on what a grade is, we will continue to how to calculate grades.
-
After grading an exam or assignment, you usually end up with a score, which is a number of points. Now, you have to decide on the grade that corresponds to the points, that is, you do a score-grade transformation.
Possible formulas for score-grade transformation in open questions (graphical representation in Figure 2):
Light blue squares: \(\text{Grade} = 1 + 9 \cdot \left( \frac{\text{score}}{\max(\text{score})} \right) \)
Dark blue triangles: \(\text{Grade} = \max \left\{ 1; 10 \cdot \left( \frac{\text{score}}{\max(\text{score})} \right) \right\} \)with Grade the calculated grade, score the obtained score by the student, max(score) the maximum obtainable score for the assessment, and max{a;b} the maximum value of a and b.
The method you choose will determine the cut-off score: the number of points a student needs to obtain in the exam in order to obtain the minimum pass grade.
In Figure 2, for the light blue squares, grade 6.0 corresponds to collecting 55% of the points, while for the dark blue triangles, 60% of the points will assign the student grade 6.0.
The examiner will communicate the cut-off score or the score-grade formula on an exam’s cover page or in the assessment instructions.
-
When calculating the grade for MCQs, you can adjust the grade to compensate for guessing. This is called ‘guessing correction’. Statistically speaking, students who are unfamiliar with the course content can score a percentage of correct answers that is inversely related to the number of answer options.
You should check if the guessing correction is mandatory/advised in the assessment policy of your faculty or programme. The reason for applying a correction for guessing can be found in quality requirement reliability, which implies that the question type (open, closed, etc.) should not influence the grade. If students do not know anything about the course content, they should get a grade of 1.0, regardless of whether the exam had open-ended or closed-ended questions.
For example: in case of 4 options (1 correct answer and 3 distractors), the guess correction is ¼ = 25%, and for true/false questions, the guess correction should be 50%. For an exam with 54 questions, with 3 options each the guessing correction is 33.3% * 54 = 18 points. Grade = 1 + 9 * (points – guessing correction)/(54 – guessing correction) = 1 + 9 * (points – 18)/36.
If it were an open question exam, they would get 0 points.
Because you want your students to get the same grade for an MCQ-test as for a test with open-ended questions (for reliability), you would subtract the number of points they can earn by guessing, from the total score. In the score-grade transformation of MCQs, the guess correction should be considered, such that the students will have no points (or a 1) whenever their score is equal or lower than the guessing correction.
Possible linear formulas for score-grade transformation for closed-ended questions are:
\(\text{Grade} = \max \left\{ 1; 1 + 9 \cdot \left( \frac{s - gs}{ms - gs} \right) \right\} \)
\(\text{Grade} = \max \left\{ 1; 10 \cdot \left( \frac{s - gs}{ms - gs} \right) \right\} \)
with 𝐺𝑟𝑎𝑑𝑒 the resulting grade, 𝑠 the obtained score by an individual student, 𝑔𝑠 the guessing score (average obtained score of random guessing), 𝑚𝑠 the maximum score, and max{𝑎;𝑏} the maximum value of a and b.
-
The previous grade calculations automatically resulted in a cut-off score.
You can also decide on an appropriate cut-off score yourself. The cut-off score should reflect the minimum level that students should have reached in order to pass the course. You determine this score by determining for each subquestion how many points a student with a 6 would on average gain for this question. The sum of this is the cut-off score. This then should pave the way for students to pass follow-up courses, and achieve the exit qualifications of the programme to an acceptable level.
In the next paragraph, you read how to set the cut-off score manually.
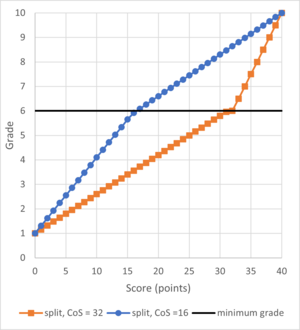
If you want to set the cut-off manually, you will need to split the score-grade transformation around the cut-off score. In Figure 3, you can find a graphical representation of split score-grade transformations with a cut-off score of 16 points (blue circles) and 32 points (orange squares) respectively. This representation is for closed-questions.
Used formulas for split transformations:
\(\text{Grade} = \begin{cases} 1 + \frac{s}{\text{CoS}} + \frac{5}{\text{CoS}}, & s < \text{CoS} \\ \frac{6ms - 10\text{CoS} + 4s}{ms - \text{CoS}}, & s \geq \text{CoS} \end{cases}\)
with 𝐺𝑟𝑎𝑑𝑒 the resulting grade, 𝑠 the obtained score by an individual student, 𝑔𝑠 the guessing score (average obtained score of random guessing), 𝐶𝑜𝑆 the cut-off score and 𝑚𝑠 the maximum score.
-
In exams, the knowledge percentage is the percentage of questions that a student should be able to correctly answer to reach the cut-off score and minimum pass-grade.
For multiple choice questions the cut-off score is higher than the knowledge percentage times total number of questions.For example, if you want your students to answer at least 60% correctly of an open-ended question (i.e. knowledge percentage is 60%), your cut-off score in case of MCQs with 4 options needs to be 25% (guessing score) + 60% (knowledge percentage) x 75% (100% - guessing score = remaining score) = 25% + 45% = 70%. In other words, students will get a pass when they correctly answer 70% of the questions (cut-off score), for a knowledge percentage of 60%.
Consider the following questions:
- At pass level, what knowledge level (%) do students have?
- Is a knowledge percentage of 60% too low and should the students meet more criteria per learning objective to deserve a pass?
If the learning objective is to design a bridge, is it enough if the students meet 60% of the design specifications, or is it important that all of them are met? What impact could it have on their careers if they only meet 60% of the requirements? How much will they use what they have learned in your course? What year are the students in? Will there still be a course that builds on this learning objective or is your course the last one in the programme where your students should perform on the level of the exit qualifications of the programme? What are these exit qualifications (you can find them in your programme’s TER)?
-
How difficult should an exam or assignment question be? It depends on whom you are asking. From an item analysis point of view, it is best if the average score is low, for example 50% (i.e., with a p-value of 0.5). However, it might make students and lecturers feel demotivated when on average only half of the questions were answered correctly. Furthermore, students should demonstrate what they are able to do during an exam, and not what they are not able to do.
For both the students and lecturers, it is important to distinguish correctly and consistently between a 6, 7, 8, 9 and 10. These grades could give a good indication of the student’s level of achievement. On the other hand, a 1, 2, 3, 4 and 5 all result in a ‘fail’, regardless of the grade. If 58% of your points would lead to a 5.8 (pass), that would mean that you have only 42% of the exam points left to distinguish between the range of 6-10.
Let us say that your exam has 40 points to divide in steps of 1 point, that would mean that a change of 1 point changes the grade by (10 (maximum grade) – 1 (minimum grade)) / 50 (total points) = 0.225. This means that the step-size of one point is 0.225 grade. If you would have 60% of the points left (i.e. a cut-off at 40% of the points), the step-size will be smaller for the pass grades, i.e. (10 – 6 (minimum pass grade)) / (60% x 40) = 0.17 points, and coarser for the fail grades, i.e. (6 – 1) / (40% x 40) = 0.31.
If you choose a lower cut-off score, you have more points left to distinguish between the grades of 6, 7, 8, 9, and 10. 50% of the points could imply a 7.0, for example. One way to do this is to determine the number of points at which a student will have a 6.0 (the cut-off score). You can then linearly interpolate between 0 points (1) and the cut-off score (e.g. 15.0 points, 6), and between the cut-off score (15.0 points, 6) and the maximum score (40.0 points, 10). The gradient of the line changes at the cut-off score: the line is shallower between the cut-off score and the maximum score.
If this exam would be very difficult but would still result in a high pass rate, due to the low cut-off score, this could imply that students would pass while they could answer only very little questions. This may demotivate students quite a lot (and may demotivate you too, while grading). Furthermore, constructive alignment and transparency demands that your students practice with questions that are at the same level as the exam. You and your students would be worried if they would only be able to answer 50% of the questions after having completed your course.
To conclude, theoretically, students should on average score 50% (p = 0.5) on all questions, and you can choose a cut-off score below 50%. However, aiming for an average score of 50% might leave both students and graders depressed. Find a mix of both challenging and few easy questions, that will help you to distinguish grades between 5.0 and 10.0. Make sure that the easy questions cannot be answered without actively participating in your course.
-
If your exam consists of open-ended and closed-ended questions, you are recommended to calculate a grade for the open-ended questions, and a grade for the closed-ended questions separately. Then, for the grade calculation of the closed-ended questions, also, you must consider the guessing correction. After calculating both grades, you calculate the total weighted average. Communicate the weighting of both grades to your students (before, during and after the exam). It is helpful for students to know the separated grades, too, since it gives them feedback on what type of questions they need to focus on most during their preparation for future assessments.
The reason why you need to calculate the grades separately, is so a guessing correction can be done on the points of the closed-ended questions. The following example will illustrate why you are advised to calculate the two grades separately.
Let’s assume that the exam consists of 100 points:
- 60 points to be earned in open questions
- 40 points divided over 40 MCQs with four alternatives
- In order to correct for guessing, 10 points need to be deducted from the score.
Now let’s assume that one of your students did not get any points for the MCQs (0 points) and full points for the open questions (60 points).
Firstly, consider the situation in which you apply guessing correction, and calculate a combined grade at once. Because of the guessing correction, the corrected amount of points would be 50 (60 – 10 points), out of the maximum of 90 points (100 – 10 points). Depending on the calculation, this would lead to the student attaining a 6.0 or a 5.6.
Secondly, if you apply guessing correction and calculate separate grades, the grade varies between 6.0 and 7.0, depending on the ratio of the weights of the open question grade and closed-ended questions. The technical reason for the difference is that in case of combining the grades, the grade for the closed-ended questions is virtually negative.
However, in order for the grade to represent the level of learning objective achievement, it is undesirable to have negative grades, especially since the grading of closed-ended questions should be comparable to the grading of open questions. For an open (sub)question in an exam, you would not give negative points when a student would not fill in anything for a certain subquestion, nor when he would have made an enormous amount of errors within this subquestion. The minimum amount of points per subquestion is 0.
Concluding: In order to prevent (virtual) negative grades (or points) in case of guessing correction, you are advised to use the weighted average of the MCQ grade and open question grade.
Table 6. The influence of grade calculation decisions on grades for exams with a combination of open and closed-ended questions, for three hypothetical students with different scores for both question types. Ratio open scores vs MCQs: 60:40
Guessing Correction Separate grades or single grade? Grading student A Grading student B Grading student C open questions: 60/60
MCQs: 0/40open questions: 60/60
MCQs: 10/40open questions: 30/60
MCQs: 20/40Grade open questions Grade closed questions Total grade Grade open questions Grade closed questions Total grade Grade open questions Grade closed questions Total grade Separate grades 10.0 1.0 6.4 10.0 1.0 6.4 5.5 4.0 4.9 Single grade 10.0 -2.0 6.0 10.0 1.0 7.0 5.5 4.0 5.0
2.3. Objectivity and reliability of grading
In this section, objectivity, or the reliability of the grade is discussed, as well as possible solutions for errors made by assessors. Because we are all human, it is nearly impossible for anybody not to occasionally make errors while grading. There is also even more room for errors when more than one assessor is grading the same assessment - different assessors will simply grade differently. When assessing your students, it is important to at least be aware of this, and to take certain measures to prevent inconsistencies.
-
Student grades often partially depend on which assessor graded the work. This is mainly because the following happens during grading:
- Generosity errors: assessors are (too) lenient;
- Severity errors: assessors are (too) strict.
To help prevent, or at least diminish these errors, it is recommended to follow these guidelines:
- Use a detailed answer model or rubric. This leaves less room for assessors’ own interpretation.
- Use two assessors per sample of students’ work to even out differences in interpretation.
- Distribute the questions - not the students - over the assessors. This way all students are evaluated equally generous/strict.
- Have a session in which all assessors discuss the meaning of the answer model. Then grade a few samples of students’ work and discuss and resolve any differences in rating. Only when everyone seems to interpret the results consistently, the actual grading can begin.
-
When there is just one assessor who evaluates all students’ work, there are a number of factors that endanger objective and reliable evaluation of students’ 25 Grading results. Here are three examples and the measures that can be used to avoid them:
- Halo and horn effect:
The assessor allows their general impression of the student to influence the scores.- Mark the test anonymously by having students only write their student number on the answer sheets.
- Let someone who does not know the students evaluate the results.
- Have two assessors - one of whom does not know the students - evaluate the results.
- Use an answer model or a rubric.
- Contrast effect:
the assessor over- or underrates students' work because of the quality of other students' answers that were graded previously.- Use an answer model or a rubric.
- Evaluate per question – not per student, and change the order of the students per question.
- Rescore the first few samples after you have finished all. The first ones are usually scored more strictly then the rest.
- Sequence effect:
there is a shift in standards, or the scoring criteria are redefined over time.- Use an answer model or a rubric.
- Evaluate per question – not per student, and change the order of the students per question.
- Halo and horn effect:
References
For a list of references used in creating this manual please visit this page.