Damien Mulder
Geomatics
Automatic repair of geometrically invalid 3D City Building models using a voxel-based repair method
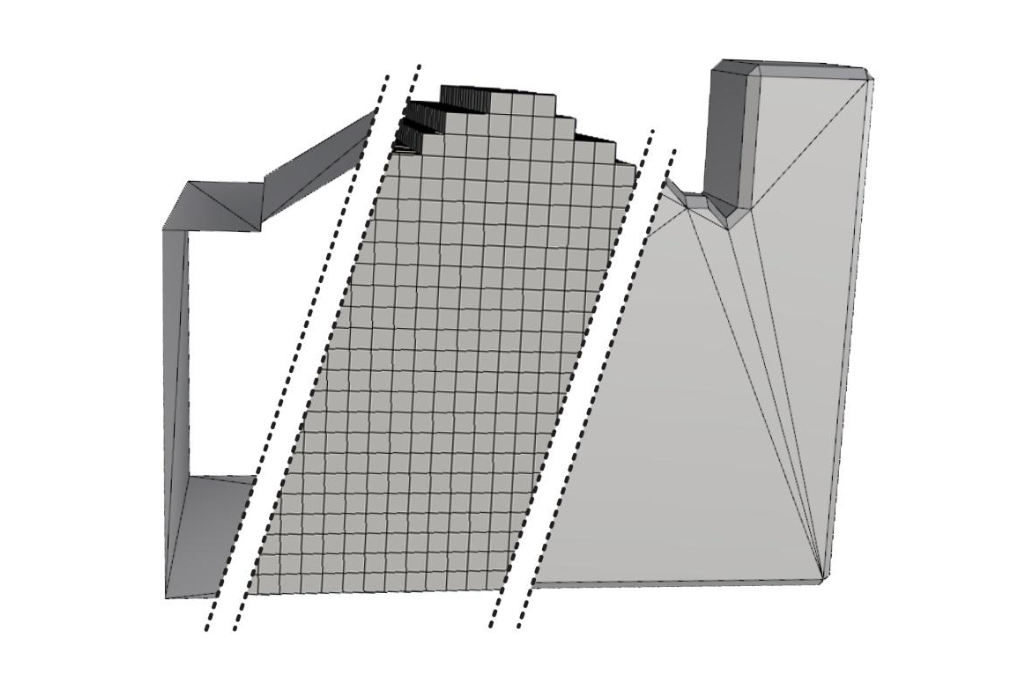
In recent years, the concept of 3D city models has been gaining in importance as more 3D geometry of urban areas is becoming available. Although 3D City models offer a structured way of storing geometry, in practice a significant amount of geometry is not considered valid. This hinders the further analyzing or processing of these models. Since manual repair of 3D City models is very time consuming and prone to errors, automatic repair methods are highly desirable. However, none of the existing repair methods are able to entirely repair all defects in 3D City Models. This thesis focuses on the process of transforming a defect 3D city model into a valid one by using a voxel-based repair method. The first step of this process is the scan conversion of a (defect) 3D building model into a volumetric representation. By applying a set of morphological operators, a single volume without holes can be acquired.
The second step is to reconstruct a triangle mesh for a given volumetric representation. Two workflows are proposed to perform this step. The first workflow is based on the Marching Cubes algorithm, which generates a triangle mesh for a grid with binary or scalar values. The second workflow has been developed on the base of the Dual Contouring algorithm, which uses intersection points and surface normal vectors of the input model to generate a triangle or quad mesh. Finally a detriangulation is performed in the post processing, which writes the repaired model back to a polygonal 3D City model.
In order to preserve any attributes of 3D City Models throughout the repair process, three alternatives are proposed; geometry based assumption, voxel based preservation or grid edge based preservation. Each of these possibilities may be suitable, depending on the selected workflow and desired application. Both workflows were tested on existing 3D City models. Validation of the first workflow shows that using the Marching Cubes algorithm is suitable for a reliable repair method. Applying it on a dataset with 90% of defect buildings, resulted in a dataset where only 4% of the building models remained defect. It must be noted however, that during this process sharp features are rounded off and jagged surfaces may appear. The validation of the second workflow, which aims to preserve sharp features by using the Dual Contouring algorithm, often resulted in self-intersections and thus defect output models. It was concluded that more research, including an implementation of an extension on the Dual Contouring algorithm are needed in order to determine the suitability of the second workflow for the repair of 3D City Building Models.